Leetcode #102 - Binary Tree Level Order Traversal : Breadth First Search pattern

In this blog post, we will discuss a LeetCode interview pattern, Breadth-First Search (BFS), by solving LeetCode problem #102. BFS explores the breadth of each level of a tree before moving to the next level, starting from the root. In other words, it is a level-wise traversal.

A tree is a hierarchical structure of linked nodes, consisting of a root and subtrees of children with parent nodes.

BFS traversal of a tree utilizes a queue, a data structure that operates on the First In, First Out (FIFO) principle. The process begins by adding the root node to the queue. Then, for each node processed, its children are added to the queue, continuing until the entire tree is traversed.

Understanding the TreeNode class

In binary tree problems, the `TreeNode` class serves as a fundamental building block for representing nodes in the tree. Each node contains a value - val, and pointers to its left and right child nodes. Here is how the TreeNode class is structured.

class TreeNode:

	def __init__(self, val = 0, left = None, right = None):
		self.val = val
		self.left = left
		self.right = right

1. val- this attribute holds the value of the node
   

2. left - points towards the left child of the node. If the node has no left child, , it defaults to None
   

3. right - points towards the right child of the node. If the node has no right child, it defaults to None

   
   

Level Order Traversal Algorithm

Level order traversal is an application of Breadth-First Search (BFS), specifically designed for traversing binary trees. In this traversal method, we explore the tree level by level, starting from the root and moving downward. Each level is processed completely before moving to the next, ensuring a breadth-first approach.

To implement level order traversal, we use a queue data structure, which helps maintain the order of nodes to be processed. Let’s break down the process step-by-step, beginning with the root node (1).

We start with the binary tree and initialize:

• queue: Empty

• result: Empty
  

The first step is to add the root node (1) to the queue. This sets up the traversal process.

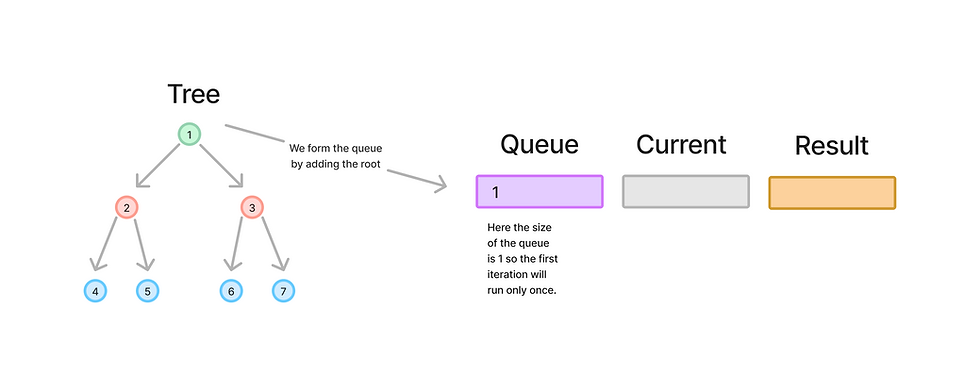
The queue now contains the root node (1). The size of the queue is 1.

	if not root: # Edge case
		return []

	result = []
	queue = [root]

Begin a while loop that runs as long as the queue has elements. This ensures all levels are processed.

The first step we follow is to get the size of the queue currently. We then create an empty array called current_level to store the nodes being processed at this level.

Remember the size of the queue is 1 in our example iteration, which means this iteration will process one element (node 1).

	while queue:
		level_size = len(queue) 
		current_level = []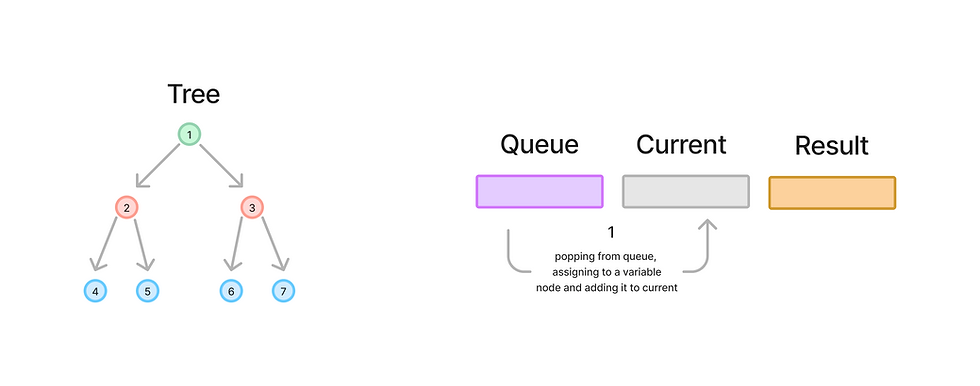

		for _ in range(level_size):
			node = queue.pop(0)

			current_level.append(node.val)

			if node.left:
				queue.append(node.left)

			if node.right:
				queue.append(node.right)

We pop the first element (1) from the queue.

• We add the value of node 1 to the current_level array.

• We then check for its children:
  

  • The left child is 2, so we add it to the queue.

  • The right child is 3, so we add it to the queue.
    

At this point:

• queue: [2, 3]

• current_level: [1]

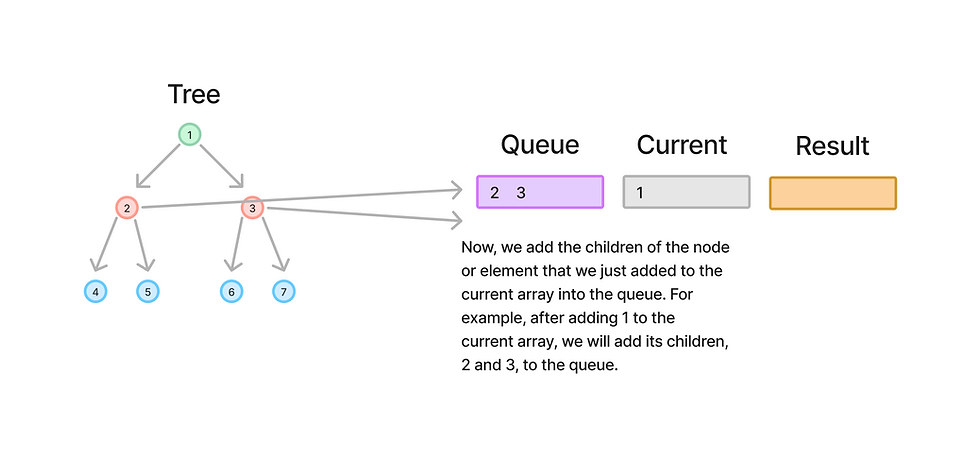
The processing for node 1 is complete, and there are no more elements in the queue for this level.

• We add the current_level array [1] to the result array.

  
  

		result.append(current_level)

At this point:

• queue: [2, 3]

• result: [[1]]

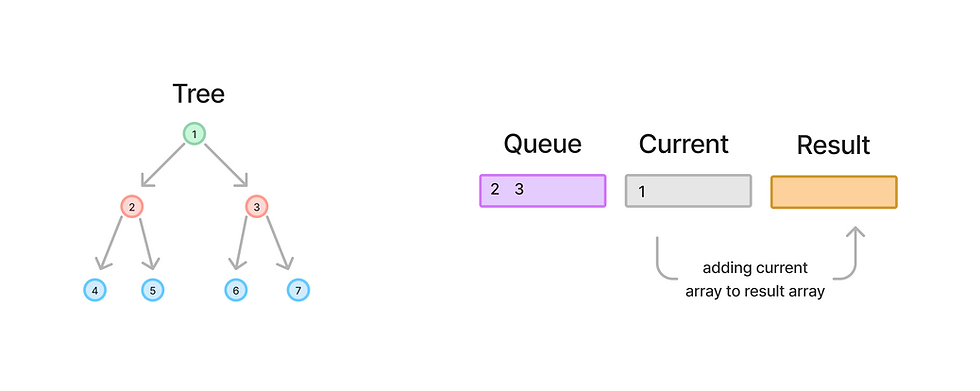
The result array now contains the first level of the tree (1) as a nested list. This completes the iteration for node 1.

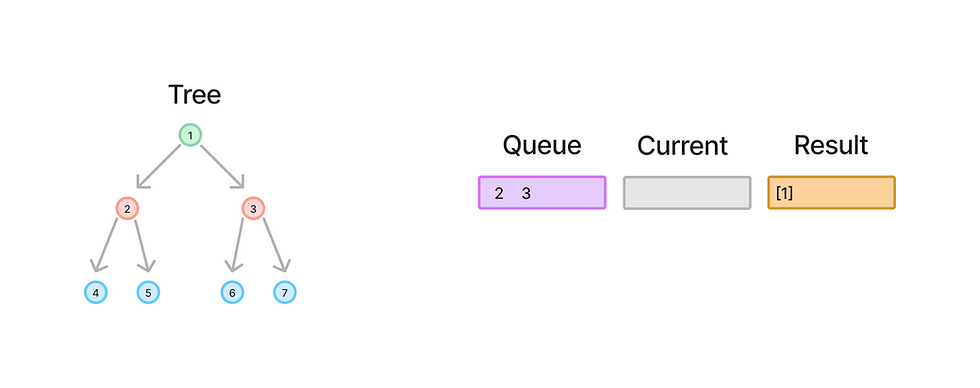
With node 1 added to the result, we are now ready to proceed to the next iteration, where nodes 2 and 3 will be processed.

We will now repeat the entire process for the elements in the queue: pop them, add them to the current array, and then add their children to the queue.



For example for next iteration the current array will be made up [2, 3] and 4,5,6,7 will be added to the queue

Level Order Traversal Python Code

Before we write the code, let's revise the algorithm once.

1. Set up the traversal process with result and queue array
   

2. Begin a while loop that runs as long as the queue has elements. This ensures all levels are processed.

2. In each iteration of the while loop, check the size of the queue (level_size). This represents the number of nodes in the current level.


• Create an empty array (current_level) to store the values of the nodes at the current level.


• Use a for loop that iterates level_size times (once for each node in the level).


• In each iteration:

• Pop the first node from the queue.

• Add the node's value to current_level.

• If the node has a left child, append it to the queue.

• If the node has a right child, append it to the queue.


3. After exiting the inner loop, append current_level to the result array.


The queue now contains all the nodes for the next level, and the outer while loop repeats.

def binary_tree_level_traversal(root: TreeNode) -> List[List[int]]:

	if not root:
		return []

	result = []
	queue = [root]

	while queue:
		level_size = len(queue)
		current_level = []

		for _ in range(level_size):
			node = queue.pop(0)
			current_level.append(node.val)

			if node.left:
				queue.append(node.left)
			if node.right:
				queue.append(node.right)

		result.append(current_level)

	return result

Time and Space Complexity

Time Complexity

The time complexity of the function is O(n), where n is the number of nodes in the binary tree. Here's why:

1. Each node in the tree is visited exactly once when it is dequeued and its children are enqueued.
   

2. The operations within the while and for loops (e.g., appending to current_level, adding children to the queue) are constant-time operations for each node.
   

3. Therefore, the algorithm processes each node in the tree exactly once, leading to a linear time complexity of O(n).
   

Space Complexity

The space complexity of the function is O(m), where m is the maximum number of nodes in any level of the tree. This is because:

1. The queue can hold at most all the nodes in a single level at any point in time.
   

2. For a perfectly balanced binary tree, the maximum number of nodes in the last level is approximately n/2, where n is the total number of nodes.
   

3. Thus, the space complexity is proportional to the width of the tree, which is O(m).
   

Summary

• Time Complexity: O(n)
  

• Space Complexity: O(m), where m is the maximum number of nodes in a level.

Conclusion

In this blog post, we explored the concept of level order traversal, an application of Breadth-First Search (BFS) in binary trees. Using a queue, we processed the tree level by level, starting from the root and moving downward. This approach ensures that all nodes at a given level are visited before moving to the next level.

We also analyzed the time and space complexity of the algorithm, noting that it runs efficiently in O(n) time and uses O(m) space. This makes level order traversal a practical and widely-used technique for problems involving binary tree traversal.

By understanding and implementing this algorithm, you’ve gained a deeper insight into how BFS can be adapted for specific data structures like trees. This knowledge is foundational for solving more complex tree problems in coding interviews and real-world applications.

Similar Problem - Leetcode Problem #103